In Part 1, I catalogued and critiqued common uses of “They’ll need it for high school.” Samuel Otten’s take on “When am I ever going to use this?” was an obvious influence. “Poor Pedagogy Preparation” was one of my categories: “I want them to get used to it” as an indefensible defence for the mad minute. Since that post, I’ve wondered about putting a positive spin on “I want them to get used to it.”
As a K-12 Numeracy Helping Teacher, I have the opportunity to teach in elementary and secondary classrooms alike. Often, I’m struck by how pedagogical similarities overwhelm any differences. Malcolm Swan’s ordering decimals lesson — a current favourite of mine — and my sinusoidal sort illustrate this.
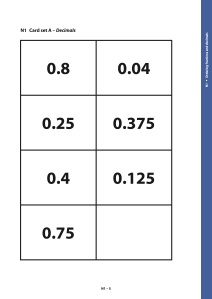
In Grade 5, students are asked to put the decimal cards in order of size, smallest to largest.
The most common response is 0.4, 0.8, 0.04, 0.25, 0.75, 0.125, 0.375. This can be explained by how students compare whole numbers. Misconceptions are revealed, but not corrected. (The rest of the activity will take care of that.)
In Grade 12, students are asked to put the equation cards in piles.
The most common response is to make two piles: sine and cosine. This can be explained by how students were introduced to y = sin x and y = cos x. This isn’t a misconception; there is no “right” sort. But it is unsophisticated. And it goes unchallenged. (The rest of the activity will take care of that.)
In Grade 5, students match hundred grids and number lines to their decimals. They explain how they know that the cards make a set, building connections between decimals and their understanding of fractions and place value. They argue. When there’s consensus, students are again asked to put the cards in order. I note their strategies that emerge (benchmarks, place value, equivalent decimals) for a class discussion.
In Grade 12, students match graphs and characteristics to their equations. They make conjectures. They explain how they know that the cards make a set, building connections between transformations of trigonometric functions and their understanding of transformations of other functions. When there’s consensus, students are again asked to put the cards in piles. I note their sorting rules that emerge (amplitude, period, phase shift, vertical displacement, range, maximum/minimum values) for a class discussion.
Elementary and secondary lessons need not be as closely aligned as above. It’s not about matching card matching activities. Or parallel “Which one doesn’t belong?” prompts. Or three-act math tasks for K-5. More generally, exploring and discussing ideas, working collaboratively in pairs/small groups, problem solving (and posing!), … you could make a case for students needing these experiences in elementary school because… wait for it… they’ll need it for high school. We want them to get used to it. I hope.
A nagging thought… I’m not convinced that pedagogy preparation is ever a satisfactory response to “So, what will they need?” Even if that pedagogy is positive. If we’re going to follow that pathway, then this question demands an answer not in terms of teaching methods but in terms of the mathematical habits of mind (or processes or practices or competencies) that these teaching methods aim to promote. (See my “Affective Domain” concerns in Part 1.)
That’s not to say that I wasted my time with this post. For me, it’s always helpful to think about and present examples of secondary mathematics education as something other than passive. Maybe that — reframing those pedagogical “TNIFHS” conversations with colleagues into something more promising — is the real value here.