Gotta be 3 & 10! Or 4 &9. Balance and rotational symmetry.
Back in September, I shared Howie’s tweet with my daughters and am relieved to report that they, too, answered correctly. This is an ongoing thing with us. Whether eggs or cookies, what’s left should either (a) represent a pattern or (b) illustrate a mathematical concept. It’s these mathematical concepts that inform how I create or select a number talk image. There’s a purpose for each image.
Consider the following arrangement of macarons…

You might see six groups of six, each group its own flavour (left to right: crème brûlée, dulce de leche, pistachio, red velvet, chocolate & mandarin, chocolate). Or you might see six rows and six columns — an array. If I had 18 macarons left, I could place them in three rows of six or six rows of three, demonstrating the commutative property of multiplication…


You might see the remaining macarons not (only) as 18 but (also) as one-half. (See this tweet — similar to Howie’s — for one-half of a carton of eggs left.) Expanding from left to right or top to bottom introduces equivalent fractions: 3/6, 6/12, 9/18, … 18/36. Every second row or every second column also gets you one-half. So, too, does every second macaron, whether looking across rows or down columns…

This arrangement maintains the balance and rotational symmetry of my two-eggs-left choice above. (See Simon Gregg’s symmetrical eggs tweet.) There are many interesting ways of seeing eighteen here, including 2(1 +3 + 5) on the diagonals. If a particular strategy does not emerge from the class, I often “go backwards” (e.g., “I see 2(5 + 4). How do I see them?”).
If I had thirty macarons left, I’d remove one column or row, which introduces the distributive property of multiplication…


The number of macarons in these two photos can be expressed as 6(4 + 1) and (3 + 2)6, respectively.
Sticking with thirty, removing a diagonal can bring to mind part-whole relationships as well as the associative property of addition…

Here, five is composed of zero and five, one and four, two and three, and so on. Two plus three (pistachio) is equal to three plus two (red velvet).
If I had 20 macarons left, I could choose to emphasize multiplication as equal groups — a quincunx of squares (5 × 4) or a square of quincunxes (4 × 5) — and ask What is the same? What’s different?…


Notice that if you still see rows and columns rather than groups, then you might count four rows/columns of four and two rows/columns of two. This can be expressed as 4 × 4 + 2 × 2, which calls on order of operations. So, too, does 2(4 + 4 + 2) if you take advantage of the line symmetry in each of these two arrangements.
Twenty-one macarons form a “staircase”…

Moving some of the macarons makes a “near array”: pairing chocolate with pistachio and mandarin-chocolate with red velvet produces 5 × 4 + 1 (or 6 + 5 × 3).
The Number talk images (aka “quick images” or “dot cards“) instructional routine continues to be one of my favourites. For teachers facing the challenge of facilitating this routine remotely, there are a few, albeit flawed, solutions within Microsoft Teams (SurreySchools’ supported platform).
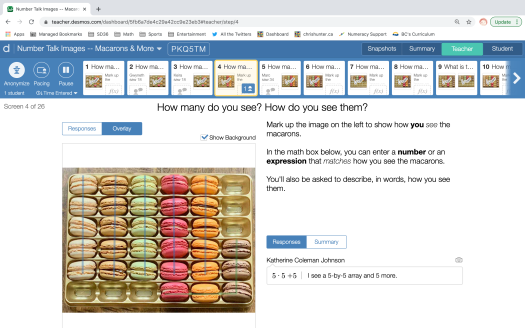
I’m with Jonathan. In Desmos, it’s dead easy to create an activity in which students can mark up an image to show how they see a quantity, enter a number or expression to answer how many, and type within a text box to explain their mathematical reasoning. Also, the Teacher Dashboard allows teachers to take and present snapshots of students’ ideas to share and discuss with the whole class. See my sample Desmos activity. It’s intended to be a template, not a single never-ending number talk. Copy and paste screens as need be. The images above — and a few more food favourites — are also included in the slide deck below.