The puck drops next week on the 2021-22 NHL season. As a hockey fan and mathematical modelling aficionado, I’m looking forward to watching Alex Ovechkin chase Wayne Gretzky’s goal record–a record I used to think was unbreakable. I was in good company:
TSN posted the above back in November of last year. Since then, Ovi went on to do two things:
- score 24 more goals (in a COVID-shortened season)
- sign a five-year, $47.5 million contract extension with the Caps
The question is less “Will ‘The Great Eight’ catch ‘The Great One’?” and more “When will he do it?” Still fun to watch but not as interesting as “Will he or won’t he?” It was uncertainties–since made certain by the offseason signing–that made it interesting, made it open to debate. There’s a takeaway for math class here.
Permit me to time travel. It’s November, 2020. Our known knowns, at that time:
- Wayne Gretzky is the leading goal scorer in NHL history
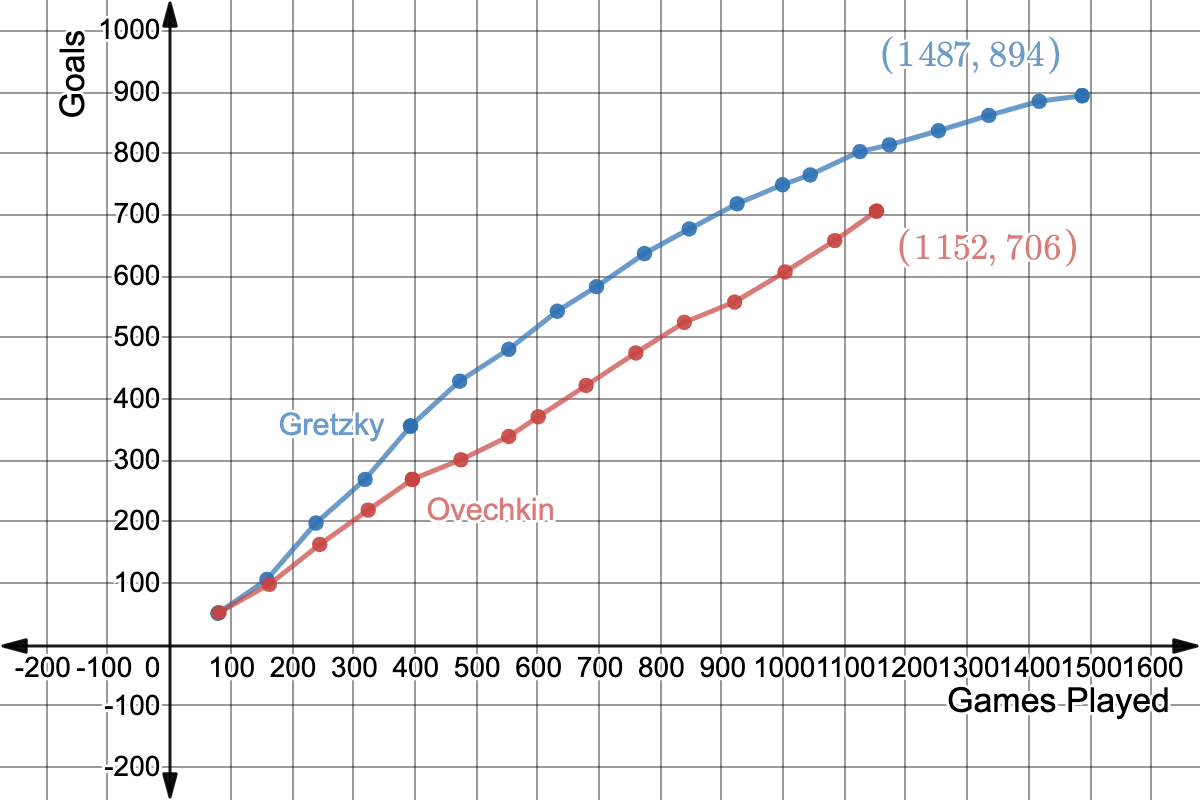
- Gretzky played in 1487 games (20 seasons)
- Gretzky scored 894 goals in his career
- Gretzky retired in ’99; he was 38
- Alex Ovechkin has played in 1152 games (15 seasons)
- Ovechkin sits at 706 goals
- Ovi’s contract will expire at the end of the 2020-21 season; he will be 35
Known unknowns:
- Ovechkin’s future goal-scoring pace
- years remaining in Ovi’s career
- where those years will be spent (i.e., NHL or KHL)
- Ovi’s future health and fitness
In BC, teachers–in all areas of learning!–are being asked to embed numeracy tasks in their classrooms. Numeracy tasks are solved using five processes–Interpret, Apply (Mathematize), Solve, Analyze, and Communicate. Outside of BC, this is called the mathematical modelling cycle.

Interpret
Here’s how BC defines Interpret:
Students are able to read and decode a range of situational contexts by identifying the real-world problems to be solved. Given insufficient or excess information, students will need to decide what information is relevant to solve the problem. This process is about students making decisions. Situational contexts may require students to identify constraints and ambiguities, and decide on next steps.
https://curriculum.gov.bc.ca/sites/curriculum.gov.bc.ca/files/pdf/assessment/gna-10-specifications.pdf
At this stage, students must understand the scenario and determine what the important variables are. Students must also make–and state–assumptions. Here, they are required to make assumptions about my unknowns above. Unfortunately–for teachers not hockey fans–Ovechkin’s new contract resolves some of these ambiguities.
Apply (Mathematize)
Students are able to identify and activate their mathematical understanding by translating real-world problems into mathematical problems (mathematizing). This process involves choosing a mathematical tool, determining how to organize the information, and creating relationship(s) in order to represent the real-world problem. (Students will need to flexibly use mathematical tools for a host of real- world problems.)
Here, that mathematical tool is likely averages/unit rates. “Likely” because students make the call about what calculations or methods to use. They may decide to use linear functions, which gives a clearer picture of the problem:
Solve
Students are able to solve mathematical problems through a variety of approaches and representations. Students may also need to check mathematical solutions to determine if their solutions make mathematical sense.
Ovechkin trails Gretzky by 188 goals (894 – 706). Again, talking November, 2020. We can play with possibilities. For example, if Ovi goes on to play four more seasons, then he’d need to score more than 47 goals per season. Or, if he continues to score at about 0.6 goals per game, then he’d need to play in a little over 300 more games.
(For readability, I’m jumbling Solve and Analyze. Solve looks more like or
. Math minus context.)
Analyze
Students are able to interpret mathematical solutions in context, such that the solutions are reasonable within the situational contexts. Students may need to assess the practicality and possible limitations of solutions, identify possible improvements to an approach, or identify other situations to which solutions can be applied. In doing so, students consider how contextual factors may affect the results. For example, students may reflect on their solutions to assess risks and address social, ethical, and environmental implications.
Students do not need to be hockey fans to check if their mathematical solutions make sense in this context. A search on NHL dot com and some familiarity with scoring being part of sportsball will suffice. You don’t have to be Chi-Chi Rodríguez to approach Fawn’s putt-putt problem.
Communicate
Students are able to clearly and precisely construct valid logical arguments to defend their decisions and assumptions, explain the tools and approaches they used, and present their solutions in context. This may require students to make recommendations and use a variety of ways (e.g., tables, graphs, diagrams, equations, symbols) to visibly represent their thinking and solution.
Some students might recognize the flaws in considering averages, especially for a skater approaching 40. For example, suppose Ovechkin plays six more seasons and averages 32 goals per season. At first glance, this feels reasonable. But it hides that he will need to outperform the average at the beginning to offset a decline at the end. It might be better to consider–and discuss–the set {42, 40, 35, 30, 25, 20}.
* * ** *** ***** ******** *************
“Ruins” in this post’s title might be a tad rough. Taking away students’ control of an important variable–the number of seasons Ovechkin will play–might push this from numeracy/modelling task to word problem (if one skate wasn’t hanging the line before). It limits how they can tinker with relationships between quantities. Still, there’s space for multiple strategies and justifications (e.g., goals per season or goals per game); there’s an opportunity for students to develop mathematical autonomy.
Alex Ovechkin is already the greatest goal-scorer in NHL history. Attaining the record is beside the point. This argument demands a different mathematical model: era-adjusted goals. But that’s for another time…
Recommended
Wolf, N. B. (2015). Modeling with mathematics: Authentic problem solving in middle school. Heinemann.
