“Okay, so, um, square both sides of…”

At that moment, three students jumped to their feet and cheered. High fives may have even been shared. I asked them what was up. They asked if we could talk about it later. (Never press here, by the way. Rookie mistake. If kids give you an out, take it.) So we did. Each student had estimated how many times I would say “Okay, so, um…” during the lesson. Their earlier excitement? I hit the highest of the three estimates.

I had completely forgotten about this episode until last spring when Canucks rookie Brock Boeser’s first ever NHL postgame interview made it into my Twitter timeline. At that time, I was helping teachers make sense of the Ministry of Education’s (MoE’s) “Process for Solving Numeracy Tasks” (a/k/a a mathematical modelling cycle). This post is a collision between the two.

Interpret

The Interpret process in this mathematical modelling cycle involves reading contextualized situations in order to identify real-world problems.

In this task, we can start with the following clip and ask “What do you notice?”

I noticed the sports clichés (NSFW). Brock Boeser’s “I just want to come here and help the team get a win” is damn close to “Nuke” Laloosh’s “I’m just happy to be here, hope I can help the ball club.” I also noticed that Boeser says “you know.” A lot. I wasn’t alone.

From here, we can develop a real-world problem by asking “What do you wonder?” or “What’s the first question that comes to mind?” My question: How many times does Brock Boeser say “you know” in the postgame interview?

Note: the starting point — in the diagram and in the video — is a situation, not a problem.

Apply (Mathematize)

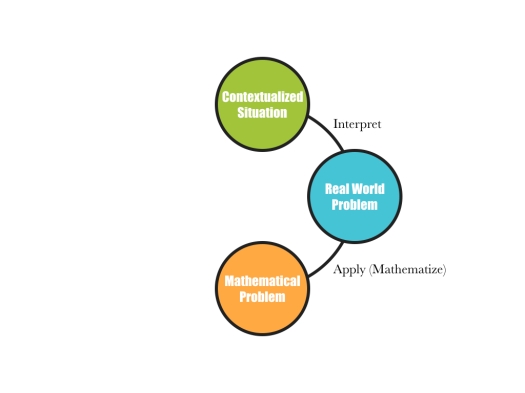
The next process involves identifying and activating mathematical understanding in order to translate real-world problems into mathematical problems. The MoE calls this Apply, a misused and abused term in mathematics education. Thankfully, Mathematize immediately follows in brackets throughout the documents.

We can ask “What information would be helpful to know here?” Students might want to know:

• the number of times that Boeser says “you know” in the clip (12)
• the length, in seconds, of the clip (44)
• the length of the entire interview (2:58)
• the rate at which Boeser says “you know” (?)
• the fraction of the time in which Boeser is speaking (?)

This process also involves — among other things — creating relationships to represent the real-world problems. Here, a proportional relationship. A simple approach might involve setting up 12/44 = x/178. A math problem.

Solve

At first glance, this looks trivial: simply cross-multiply and divide. But the Solve process involves using a variety of approaches and representations. For example, students might use scale factors or unit rates; bar models or ratio tables. Or, not proportions, but linear relations. Tables, equations, graphs. Does the solution make mathematical sense?

Analyze

Does the mathematical solution (x = 48.545454…) make sense within the contextualized situation? The Analyze process involves identifying possible limitations and improvements. Brock Boeser says “you know” 12 times in the 44 second Act 2 video. But he reaches this count at 33 seconds and finishes answering the reporter’s question at 40 seconds. Does any of this matter? Is my simple proportional approach still useful?

Communicate

Students communicate throughout the Interpret, Mathematize, Solve, and Analyze processes. This communication happens within their groups. The Communicate process in this mathematical modelling cycle involves clearly and logically defending, explaining, and presenting their thinking and solutions outside of their groups.

There are better tasks that I could have picked to illustrate this mathematical modelling cycle. In fact, last year — in the absence of sample numeracy tasks from the MoE — my go-to here was Michael Fenton’s Charge. BC’s Graduation Numeracy Assessment aside, mathematical modelling with three-act math tasks (and the pedagogy around these tasks) has played an important role in my work with Surrey math teachers for several years. The MoE did release a sample numeracy assessment in late September; I am now able to include a Reasoned Estimates, Plan and Design, Fair Share, and Model task in these conversations with colleagues. For more numeracy tasks, see Peter Liljedahl’s site.

Okay, so, um, if I didn’t pick this Brock Boeser task because it, you know, epitomizes the mathematical modelling cycle, then why did I share it? Coming full circle to the story of my three students at the beginning of this post, there’s a missing piece. Yeah, we shared a laugh and I was more self-conscious of my verbal fillers for the rest of the year (2005 ± 3). But the most embarrassing part is that I have no idea how my students came up with their estimates. Because I didn’t ask. I mean, three girls spontaneously engaged in mathematical modelling — I promise there was more mathematical thinking here than in the task at hand — and not a single question from their math teacher! In my defence, it would be several years before mathematical modelling was on my radar — an unknown unknown. Still, what a complete lack of curiosity!